Sometimes I like to work on coding problems just for fun. Things like Project Euler, Code Eval Hackerrank etc. Depending on what language you decide to do things in it might be easier and more efficient to think a little different.

Some languages like Ruby, for example, converting a number to a string with to_str() and then reversing is rather trivial. But what if I want to solve it by keeping the number a number?

Currently, I am playing around with Rust so my example will be in that language however you can use this same formula in whatever language you like.

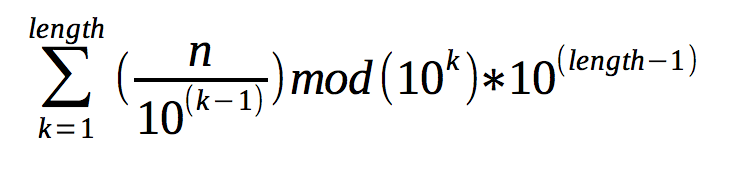
pub fn num_reverse(number: i32) -> i32 {
  let mut num = number;
  let mut rev = 0;
  while num > 0 {
    rev = rev * 10 + (num % 10);
    num = num / 10;    
  }    
  return rev;
}

Now that we have the code lets map out a little bit of how it works. Let us take the number 1234.

    num = 1234; rev = 0;

Grab the first digit.

_rev = rev * 10 + (num % 10)_ 

Which can be written as.

_rev = 0 * 10 + (1234 % 10)_  
_rev = 0 + 4_  

Then reduce num.

_num = num / 10_  
_num = 1234 / 10_  
_num = 123_  

Notice it was not 123.4, we are keeping these as integers and the divide will treat them as numbers without decimal places.

num = 123; rev = 4;

Grab the next digit.

_rev = rev * 10 + (num % 10)_  

Which can be written as.

_rev = 4 * 10 + (123 % 10)_  
_rev = 40 + 3_  

Then reduce num.

_num = num / 10_  
_num = 123 / 10_  
_num = 12_

num = 12; rev = 43;

Grab the next digit.

_rev = rev * 10 + (num % 10)_  

Which can be written as.

_rev = 43 * 10 + (12 % 10)_  
_rev = 430 + 2_  

Then reduce num.

_num = num / 10_  
_num = 12 / 10_  
_num = 1_

    num = 1; rev = 432;

Grab the next digit.

_rev = rev * 10 + (num % 10)_  

Which can be written as.

_rev = 432 * 10 + (1 % 10)_  
_rev = 4320 + 1_  

Then reduce num.

_num = num / 10_  
_num = 1 / 10_  
_num = 0_

num = 0; rev = 4321;

Now since num is 0 we can end the while loop and return rev.